During last night’s D3 presentation, I shared my Exploring Voronoi polygons and Delaunay Triangulations example and discussed some of the geometry that relates the polygons, triangles, and circumscribed circles.
At one point I showed the 4 point example, discussing how the algorithm determines whether to connect points A and C or B and D. The key is that the circumscribed circles of the resulting triangles can’t contain any of the 4 points. So, the left example is correct below and the right example is incorrect since B is inside the circle defined by triangle ACD.
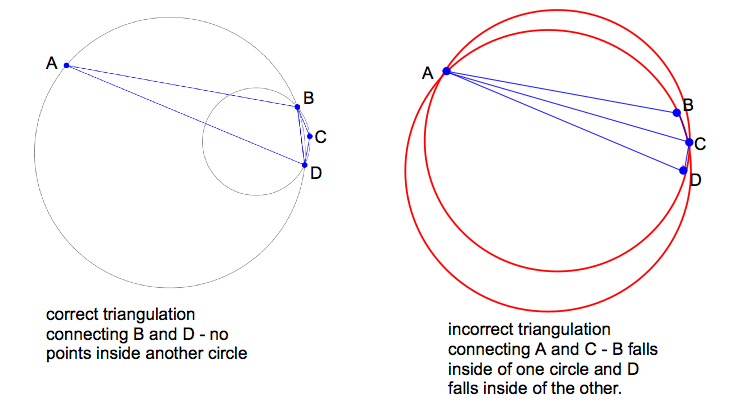
I asked the audience what they thought might define it, and somebody suggested it was the length of the connecting lines. I explained that it wasn’t, but then when I showed the example… it sort of looked like it was. The example from during the talk looked like this:
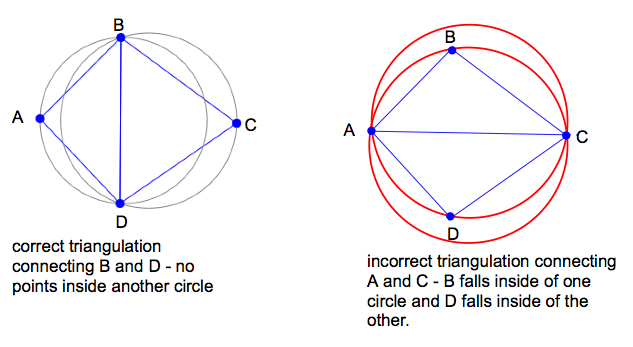
In the moment, I knew something was wrong, but couldn’t see the problem. I knew I needed to look into it more. So, I did that this morning :)
It turns out that the difference is which lengths we’re talking about. It’s not the length of the connecting line that matters. It’s the difference between the radius of the circumscribed circle.
Unfortunately when I had placed the dots during the presentation, I had accidently chosen a rare case: when the radius of the two circles was nearly equal then both the lines connecting opposite points were also both nearly equal and essentially diameters of the circle. As I brought point C closer to the center, the centerline switched from A-C to B-D when the circles were the same length. Therefore, it was easy to conflate the length of the lines and the diameter of the circles.
Looking at it again this morning, I was able to easily find an example in which the radius of the circle defined by connecting A and C was smaller than the radius of the circle defined by connecting B and D AND where the length between A and C was still longer than B and D. It becomes clear that the radius of the circle is the crucial factor and not the comparison of line lengths.
These screenshots help explain it:
At the start, it’s clear that we need to connect B and D as shown.
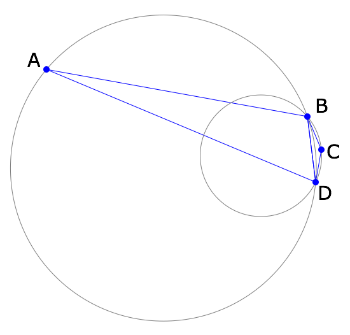
As I bring in point A, the circles become more similar in size.
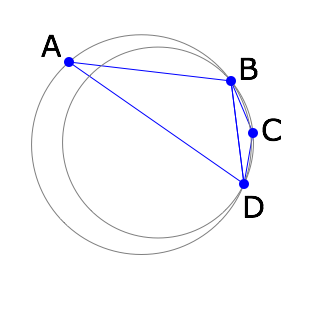
Finally, when A is too close, the triangles flip to connect A-C instead of B-D. If this hadn’t happened, A would have falled inside the circle for BCD when the radius of BCD.
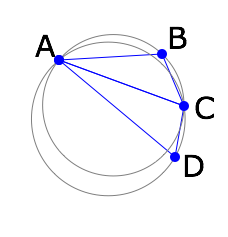
So, the triangulation is defined by the relative sizes of the circles. I believe this can also be described by the angles of the triangle, but I haven’t thought through the details. Guess I’ll be doing that next :)